《内存一致性与缓存一致性》笔记（四）：宽松内存一致性模型（上）

前两章我们讨论了两种内存一致性模型：SC和TSO，这两种模型的全局内存顺序通常都保留了每个线程的程序顺序。在这一章中，我们讨论更宽松的（更弱的）一致性模型，目的在于只保留程序员真正需要的顺序，通过允许更激进的优化（编译器或运行时）减少排序约束，进一步提升性能。缺点也很明显，需要显式地说明什么时候需要排序，并需要处理器提供相关机制，可能会影响可移植性。

动机

对内存指令进行重排的机会

什么样的顺序可以保证r2和r3始终得到NEW的值？

我们期望r2和r3总是得到NEW的值，因而需要如下顺序：

• S1 -> S3 -> L1 loads SET -> L2

• S2 -> S3 -> L1 loads SET -> L3

除了以上顺序之外，SC和TSO还会额外保证S1和S2以及L2和L3的顺序。

什么样的顺序可以保证CS1到2的顺利过渡？

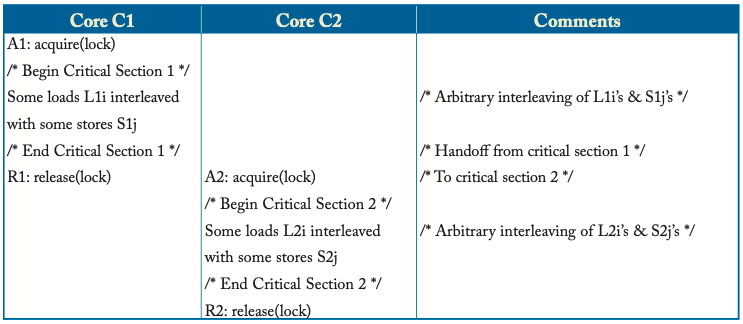
上图描述了一个更普遍的情况，即两个critical section（以下简称CS）使用同一个锁进行交接，其正确性由以下顺序进行保证：

• All L1i, All S1j -> R1 -> A2 -> All L2i, All S2j

注意正确性并不取决于CS内的load和store的顺序（除非load和store的地址相同）。在这种情况下，或许可以通过放松load和store之间的顺序来获取更高的性能。

利用重排的机会

我们现在假设有一个宽松的内存模型，我们可以对任何内存操作进行重排，并由FENCE指令进行必要的排序。这种模型需要程序员手动推理哪些操作需要排序，但也可以进行很多优化以提高性能，我们现在讨论一些常见的优化方法。

不基于FIFO的合并式Write Buffer

在TSO中我们要求write buffer必须是基于FIFO的，但一个更优化的设计是使用不基于FIFO的write buffer，且允许同一地址或相邻地址的多个store请求合并为一个store。

对乱序内核的支持更简单

在强一致性模型的系统中，一个内核可能在指令提交之前推测性地执行不按程序顺序的load，如MIPS R10000，但这样需要额外的检查流程，如MIPS R10000通过比较evict的缓存块的地址和内核已经推测性load但还未提交的地址来进行检查。相比之下，在宽松一致性模型中，内核可以不按程序顺序进行load，且不需要额外的检查。

耦合的内存一致性与缓存一致性

我们之前提倡将两个概念解耦，降低理解的复杂性，但宽松一致性模型通过“打开缓存一致性的黑盒”来提供更好的性能。例如，我们可以允许多处理器中一部分内核从之前的store请求中load新的值，另一部分仍然可以load旧的值。这种情况在现实中是有可能发生的，如一个内核上运行两个线程，共享一个write buffer，或者两个内核共享同一个L1 data cache。

宽松内存模型：XC

我们虚构了一个宽松一致性模型，称为XC。XC假设存在一个全局的内存顺序。

XC模型的基本概念

XC提供了一个FENCE指令，在没有FENCE指令的情况下，load和store都可以是乱序的。FENCE指令不指定地址，同一个核的FENCE指令之间严格顺序，但FENCE不影响其他内核的内存指令顺序。现实中的FENCE可能会附带有更多的属性，例如可以保证所有内存顺序，但是除了FENCE之前的store与之后的load。

XC内存顺序保证了以下程序顺序：

• Load -> FENCE

• Store -> FENCE

• FENCE -> FENCD

• FENCE -> Load

• FENCE -> Store

XC仅对同一地址的两个内存访问请求维护TSO规则：

• Load -> Load to same address

• Load -> Store to same address

• Store -> Store to same address

对同一地址的顺序约束还是有必要的，比如Store -> Store规则可以避免出现先执行A=1再执行A=2但结果是A=1的情况，或者Load -> Load规则可以避免出现一开始A=0且有一个处理器写入A=1时，另一个处理器上第一次load A结果为1但是第二次load A结果为0的情况。

XC保证了load立即看到自己的store请求，类似TSO的write buffer bypassing，这样保证了单线程的顺序性。

XC模型中使用FENCE的例子

在XC中使用FENCE

在XC中通过FENCE来实现CS之间的过渡

XC的形式化描述

XC的执行需要如下要求：

1. 所有内核都按如下规则将load、store和FENCE插入内存顺序<m：

   • 若L(a) <p FENCE，则L(a) <m FENCE

   • 若S(a) <p FENCE，则S(a) <m FENCE

   • 若FENCE <p FENCE，则FENCE <m FENCE

   • 若FENCE <p L(a)，则FENCE <m L(a)

   • 若FENCE <p S(a)，则FENCE <m S(a)

2. 所有内核都将相同地址的load和store请求按如下顺序插入内存顺序<m：

   • 若L(a) <p L'(a)，则L(a) <m L'(a)

   • 若L(a) <p S(a)，则L(a) <m S(a)

   • 若SL(a) <p S'(a)，则S(a) <m S'(a)

3. 每一次load都从之前最后一次相同地址的store中获取值：

   • L(a)的值为MAX_<m {S(a) | S(a) <m L(a) or S(a) <p L(a)}

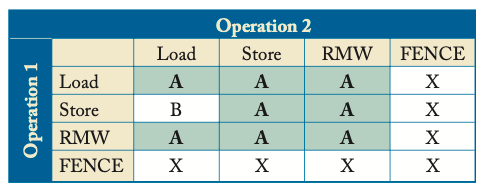XC顺序规则（X表示强制顺序，B表示访问同一地址需要bypassing，A表示只有访问同一地址才需要保证顺序）

XC如何保证程序正确执行

第一个例子中两种等价的执行方式

第二个例子中两种等价的执行方式

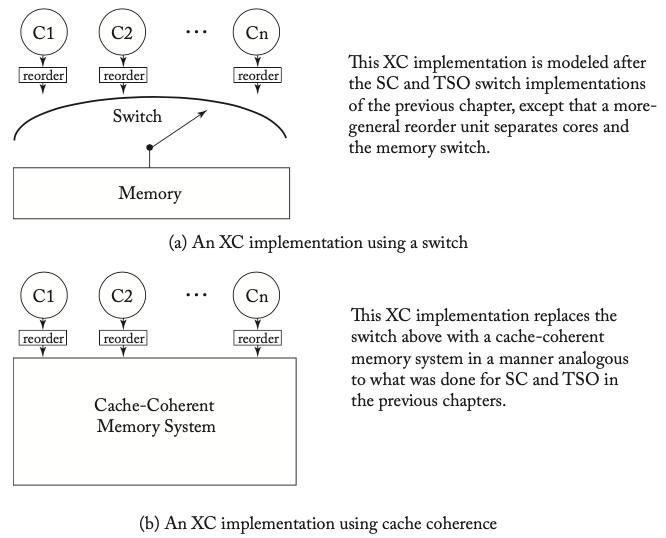
实现XC

我们采用了和SC或TSO类似的方法，也就是把内存访问请求的顺序与缓存一致性分开。在TSO中，每个内核都被一个基于FIFO的write buffer与共享内存分开，而对XC来说，这个write buffer由更一般的重排单元分开。

两种XC的实现

具体的细节和SC或TSO类似，就不详细展开了。那么，从TSO到XC这样的模型会带来多大的性能提升呢？这取决于具体的微架构实现，如之前讨论过的不基于FIFO的合并式write buffer或其他优化方法等。

实现原子指令

有几种可行的方式来实现原子RMW指令，RMW的实现也取决于系统如何实现XC。在本节中，我们假设XC系统由乱序内核组成，每个内核通过一个不基于FIFO的合并式write buffer与内存系统相连。

一个简单可行的解决方案是借用我们在TSO中讨论过的实现方式，在执行一个原子指令之前，清空write buffer，然后获得缓存块的读写权限（如M状态），然后进行load和store。但这种方案过于保守，牺牲了一部分性能。我们事实上不需要清空write buffer，因为XC允许RMW的load和store可以直接bypass之前的store。

TSO与XC实现同步的区别

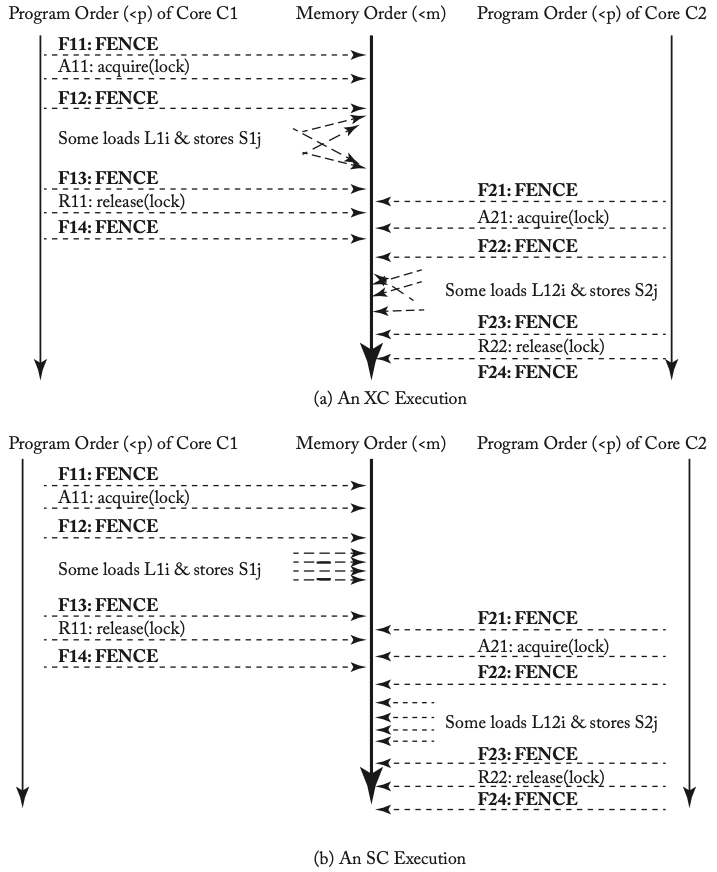
上图描述了TSO和XC实现CS的区别，在XC中，获取锁之后与释放锁之前都需要插入FENCE。

实现FENCE

有三种基本的实现方法：

1. 实现SC，并将FENCE视为no-ops。

2. 等待FENCE之前的所有内存操作完成，然后开始FENCE之后的内存操作。

3. 在前一种方法基础上实现更激进的优化，在保证顺序的前提下执行更多指令。

无数据竞争程序的顺序一致性（SC for DRF）

程序员希望既可以用简单的SC模型进行推理，又可以获得宽松模型的高性能。对于无数据竞争（data-race-free, DRF）程序而言，可以同时实现这两个目标。数据竞争的概念是，当两个线程访问同一个内存位置，且至少有一个访问是store，且中间没有同步操作。在SC for DRF中，程序员需要通过编写正确的同步指令来确保程序在SC下是DRF的，同时在架构的实现中，将同步指令映射到宽松一致性模型中的FENCE和RMW指令，实现类似SC的执行效果。XC和大多数商用的宽松内存模型都有必要的FENCE指令和RMW指令来保证SC的效果。

数据竞争的例子

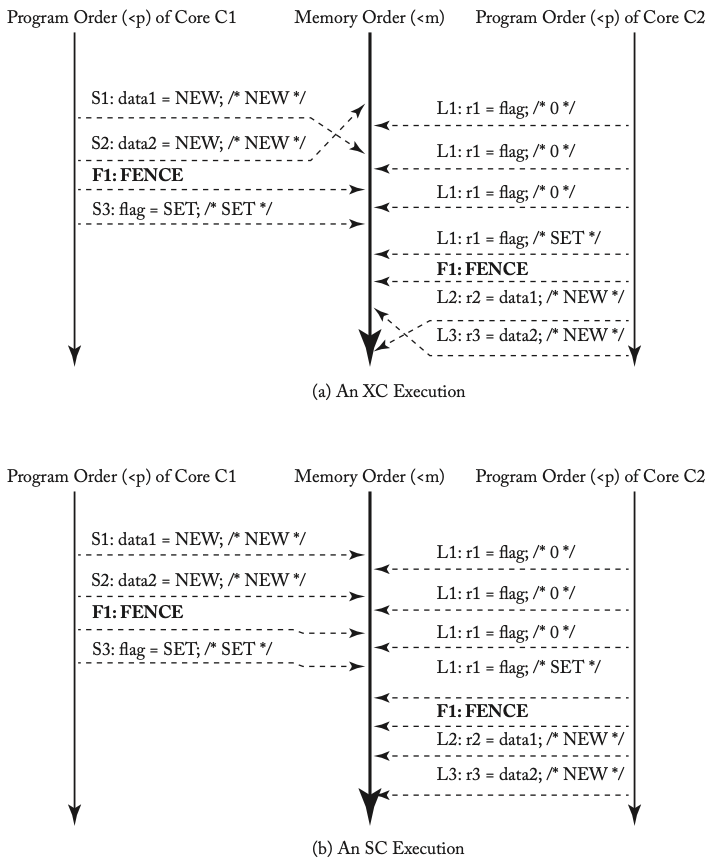
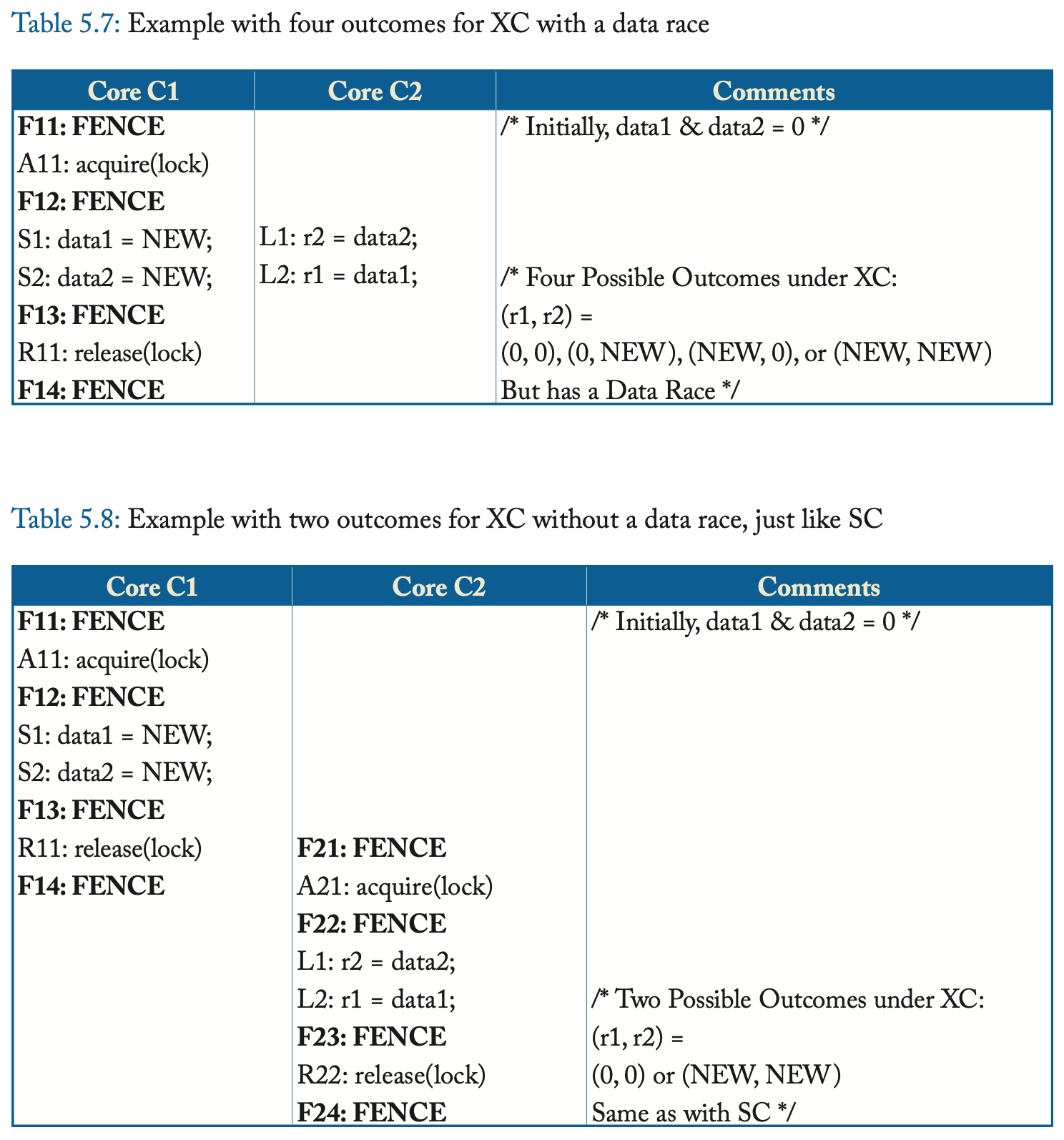
从上面的例子中我们可以看出，插入必要的FENCE之后，XC的结果与SC的结果是完全一样的。我们通过这个例子进一步讨论SC for DRF。

• 如果存在数据竞争，那么就会暴露XC对load和store的重排。

• 如果不存在数据竞争，那么XC和SC执行结果没有区别。

如果需要更深入理解SC for DRF，需要以下一些定义。

• 一些内存操作标记为“同步”，包括锁的获取和释放，其余的内存操作标记为“数据”。

• 如果两个数据操作Di和Dj来自不同的内核或不同的线程，且访问相同的内存位置，并且至少有一个是store，那么这两个数据操作发生冲突。

• 如果两个同步操作Si和Sj来自不同的内核或不同的线程，且访问相同的内存位置（如相同的锁)，并且至少有一个同步操作是store（例如，自旋锁的获取和释放会发生冲突，而读写锁上的两个读操作不会发生冲突)，那么这两个同步操作发生冲突。

• 两个同步操作Si和Sj在以下两种情况发生过渡冲突：

  • Si和Sj发生冲突，或

  • Si与某个同步操作Sk发生冲突，且Sk <p Sk'（即Sk在内核K的程序顺序中在Sk’之前)，且Sk’与Sj发生冲突。

• 两个数据操作Di和Dj发生数据竞争的条件是：

  • Di和Dj发生冲突，且

  • 在全局内存顺序中，Di和Dj之间没有过渡冲突的一对由i和j发出的同步指令（也就是说，一对冲突的数据操作Di <m Dj不属于数据竞争，当且仅当存在一对相互冲突的同步操作Si和Sj，使得Di <m Si <m Sj <m Dj）。

• 如果没有数据操作的竞争，我们就称SC执行是无数据竞争的（DRF）。

• 如果一个程序的所有SC执行都是DRF的，那么这个程序是DRF的。

• 如果所有DRF程序的执行都是SC的执行，那么这个内存模型就支持SC for DRF，这种支持通常需要特别的同步操作。

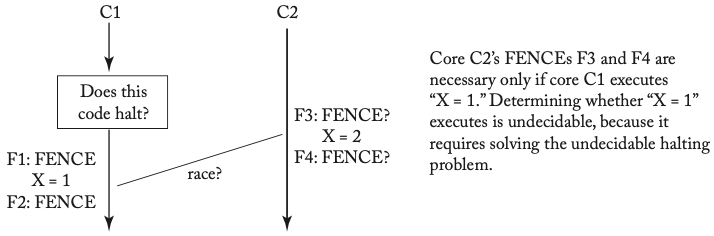
可以证明XC支持SC for DRF。为DRF程序支持SC可以让程序员直白地使用SC来进行推理，无需记住复杂的规则，同时也可以获得性能的提升，但问题在于要保证DRF程序的高性能（也就是不要把太多的操作标记为同步）也可能很困难。

插入FENCE的最优位置是不确定的

如上图所示，很难准确描述哪些内存操作可能发生数据竞争，因而必须保守地标记同步操作，插入FENCE。在极端情况中我们可能需要在所有内存操作之间插入FENCE以保证SC。同时，程序可能会因为bug而违反DRF，发生数据竞争，且在此之后可能不再遵守SC。

综上所述，程序员可以使用两种选择来推理他们的程序：

• 直接使用XC的原始规则

• 插入充足的同步指令以确保没有数据竞争，然后用相对简单的SC来进行推理

学过计算机体系结构或者操作系统课程的同学会知道，后者的应用更普遍。

一些宽松内存模型的概念

释放一致性（Release Consistency）

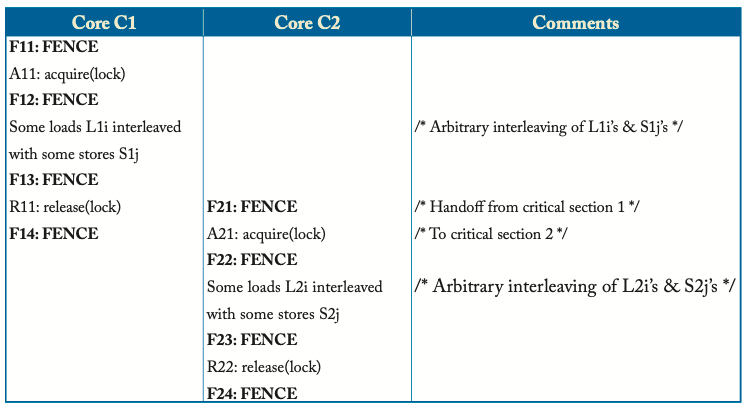
释放一致性的关键观点是，用FENCE包围所有的同步操作是多余的，对“获取锁”的同步只需要后面的FENCE，对“释放锁”的同步只需要前面的FENCE。我们回顾之前的一个例子来更清晰地说明这个概念，如下图所示。

回顾之前的例子：在XC中通过FENCE来实现CS之间的过渡

上图中，F11、F14、F21和F24可以省略。以C1的释放锁为例，F13不能省略，但F14可以，因为C1后续的内存操作在释放锁之前执行也是没有问题的。XC不允许有内存指令绕过FENCE，但RC允许这样的提前执行。事实上，RC提供了类似于FENCE的ACQUIRE和RELEASE指令，但只在一个方向上对内存访问进行排序，不同于在往前和王后两个方向进行排序的FENCE。更一般地来说，RC只要求：

• ACQUIRE -> Load, Store（但没有Load, Store -> ACQUIRE）

• Load, Store -> RELEASE（但没有RELEASE -> Load, Store）

以及ACQUIRE和RELEASE之间的SC顺序：

• ACQUIRE -> ACQUIRE

• ACQUIRE -> RELEASE

• RELEASE -> ACQUIRE

• RELEASE -> RELEASE

因果性和写入原子性

因果性：如果我看观测到了store并通知了你，你是否也一定会观测到store？

上图说明了因果性的一个例子。如果C3能保证观察到S1的完成，那么因果关系就成立，反之则不成立。

写入原子性则要求一个内核的store在逻辑上被所有其他内核观测到。根据定义，XC符合写原子性，因为内存顺序规定了一个逻辑上的原子的点，在这一点上，store请求生效，在此之前，没有其他内核可以看到store请求，在此之后，所有其他内核都可以看到store之后的值。不过需要注意的是，写入原子性允许发出store请求的内核提前看到自己的store请求。

IRIW的例子：store是否

写入原子性的一个必要不充分条件是可以正确处理独立读独立写（Independent Read Independent Write, IRIW），如上图所示。假设C3的L1观测到S1，C4的L3观测到S2，是否有可能L2的结果和L4的结果同时为0？在这种情况下，S1和S2不仅是重新排序，而是违反了写入原子性。不过，正确处理IRIW并不能推导出写入原子性。

写入原子性可以推出因果性，但因果性并不能推出写入原子性。后者的反例是，假设C1和C3两个线程共享一个write buffer，C2和C4两个线程共享一个write buffer，L1为NEW而L2可能为0，且L3为NEW而L4可能为0。