在并行编程中有一些常见的模式反复出现,这些模式都是通用的,可以在任何级别的并行和任何设备上应用,但我们仍然要考虑这些模式的某些属性(比如可扩展性),可能需要在不同的设备上微调参数,或者直接采用不同的模式来提高性能。我们在本节中主要讨论以下一些问题:
哪些模式是最重要的?
这些模式和不同设备的特性有什么关联?
DPC++函数和库已经支持了哪些模式?
如何实现这些模式?
了解并行模式
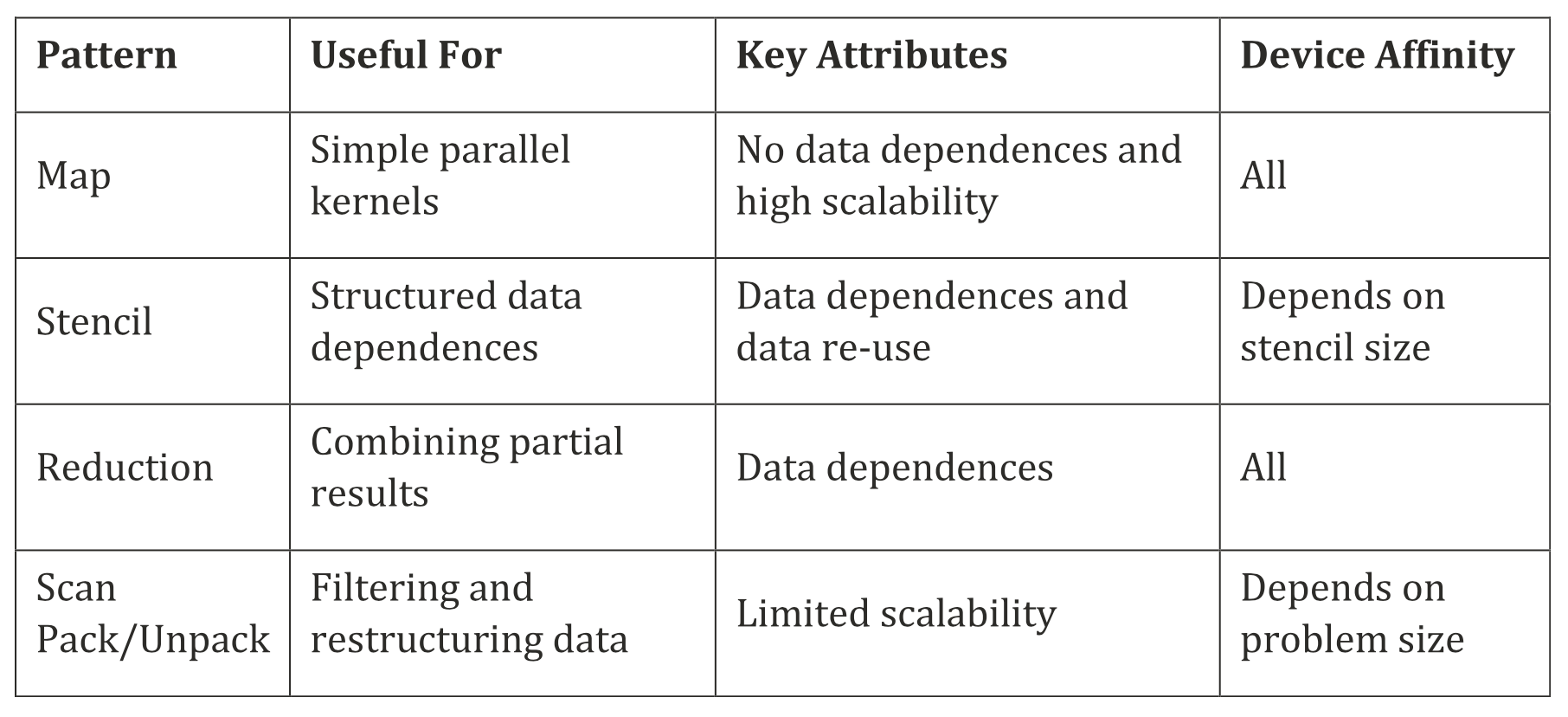
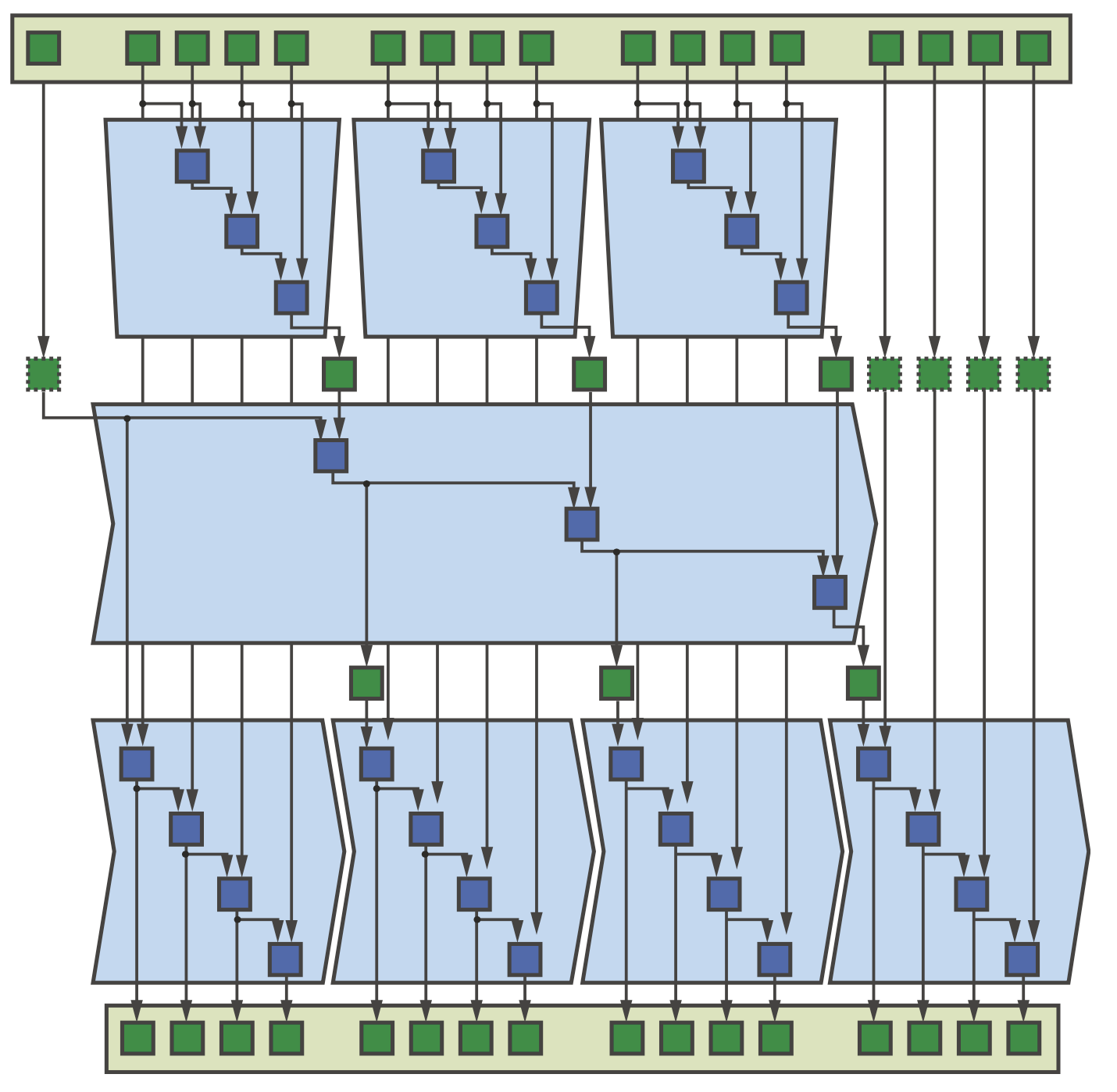
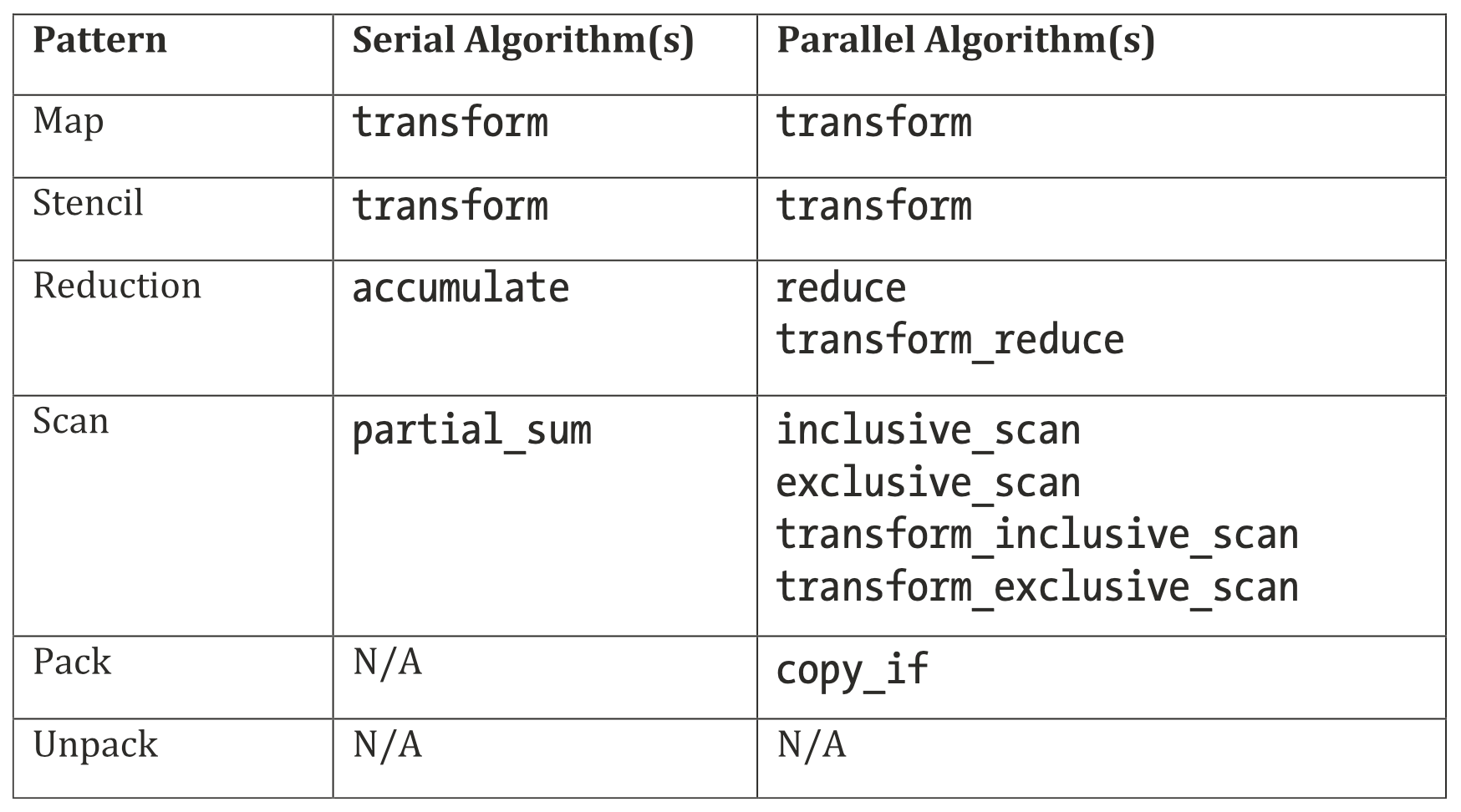
我们不讨论与并行类型有关的模式(如fork-join、branch-and-bound等),只关注对编写数据并行kernel最相关的算法模式。下图展示了不同模式的概述,包括主要用途、关键属性以及应用到设备上的能力。
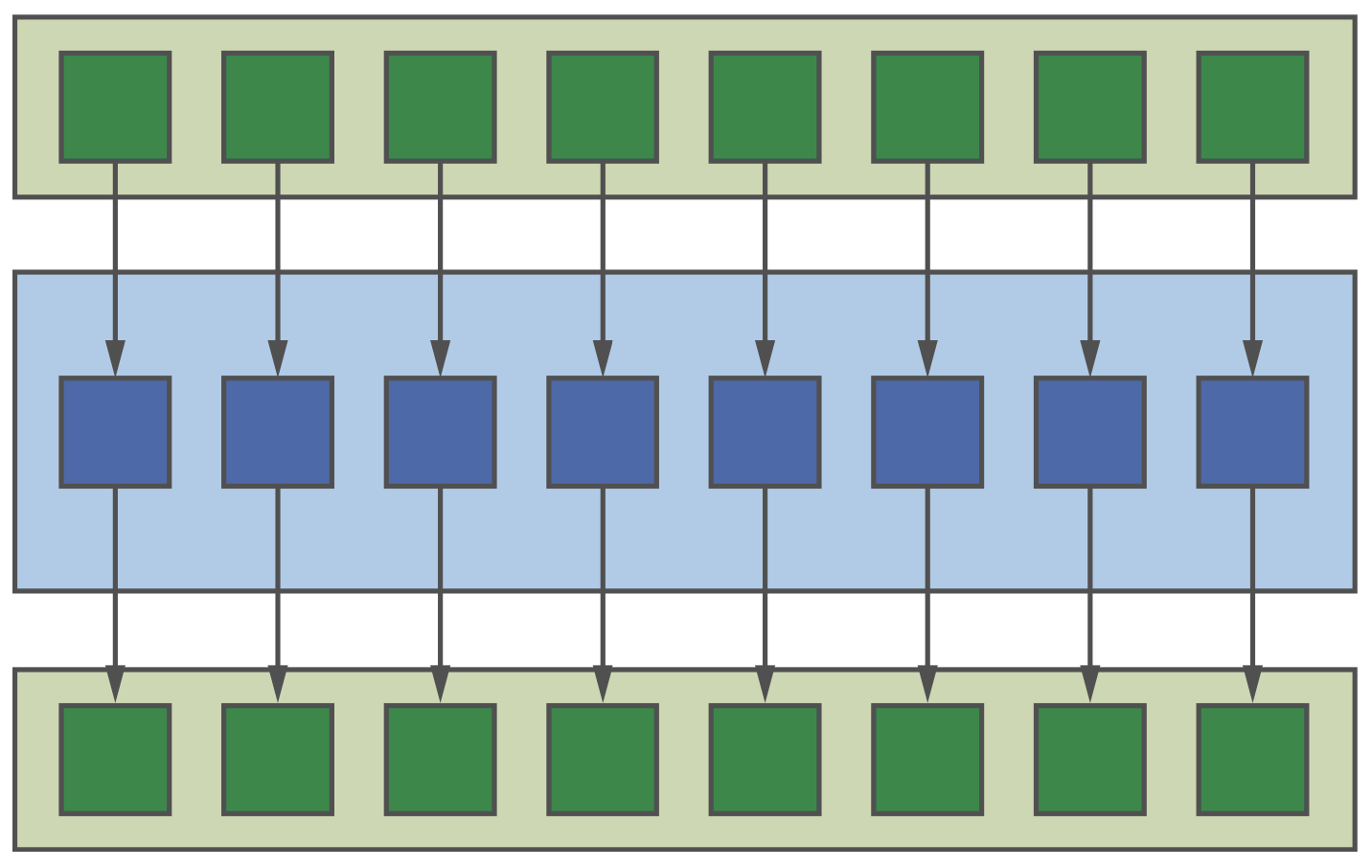
Map
这是最简单的并行模式,如下图所示。不过需要注意的是,这种模式可能会忽略一些可以提高性能的优化(如数据重用、融合kernel等)。
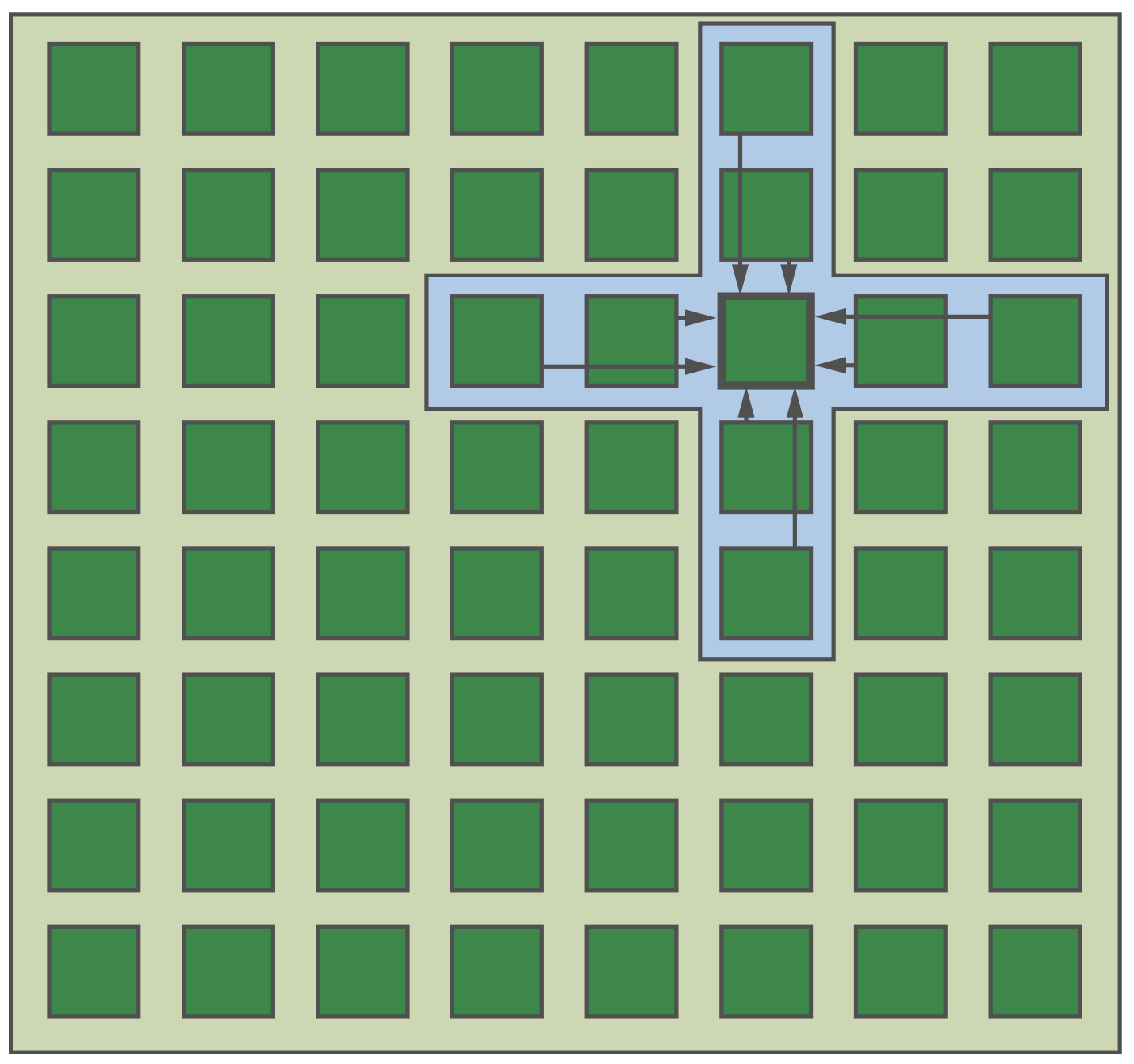
Stencil
Stencil模式如下图所示。由于stencil很容易描述,但有效实现却很复杂,因而stencil也是DSL开发中最活跃的领域之一。
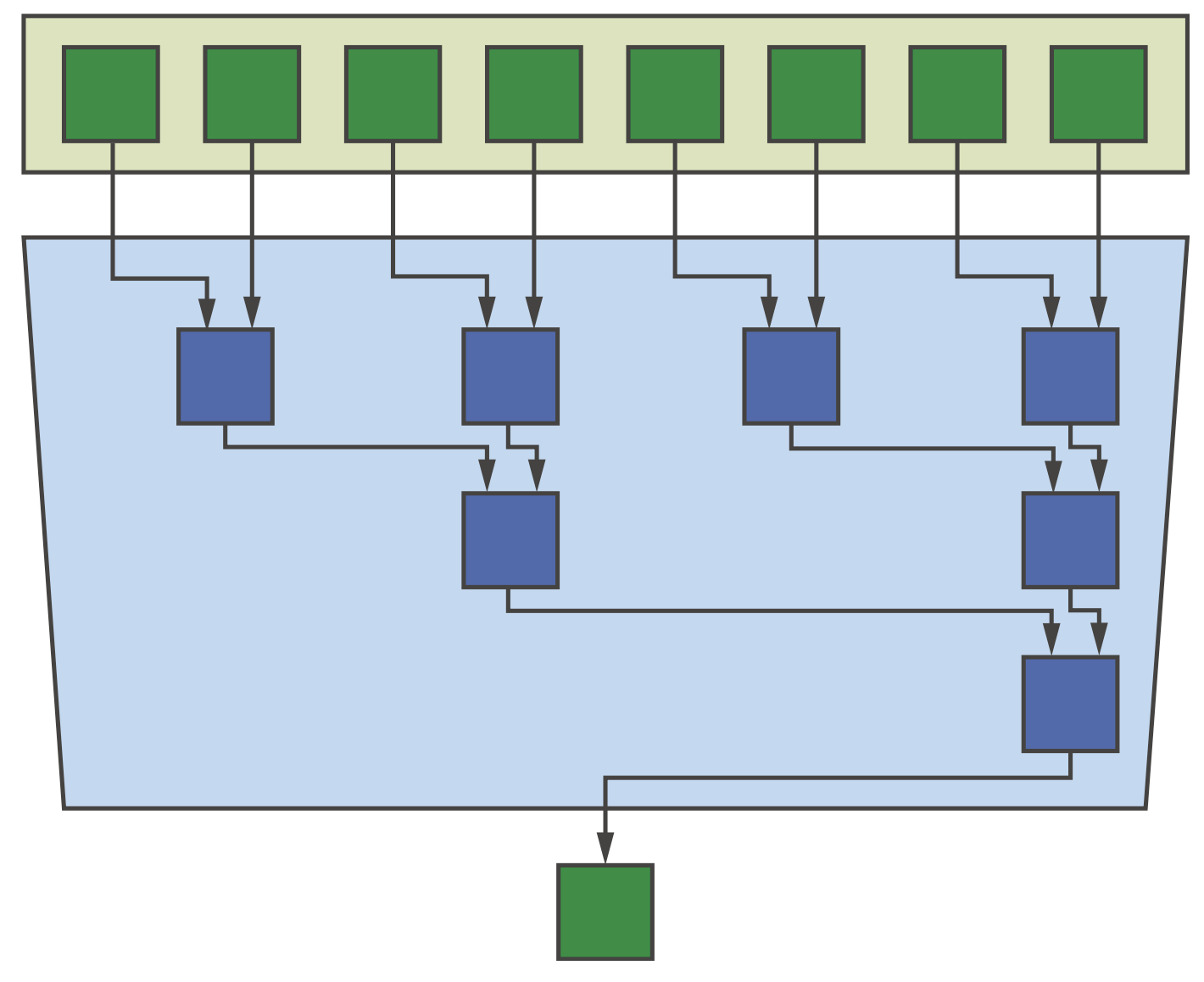
Reduction
Reduction也是一种常见的并行模式,如求和或计算最小最大值等,下图展示了树型结构的实现方法,这是一种比较流行的实现,但也有其他实现方式。
Scan
Scan使用一个二元可结合的运算符来计算广义的前缀和。Scan看起来是串行的,但仍然有潜在的并行机会(可能可扩展性较差),如下图所示。一个经验法是在产生数据的同一设备上执行扫描操作。
Pack和Unpack
这两者和scan密切相关,通常在scan基础上实现。
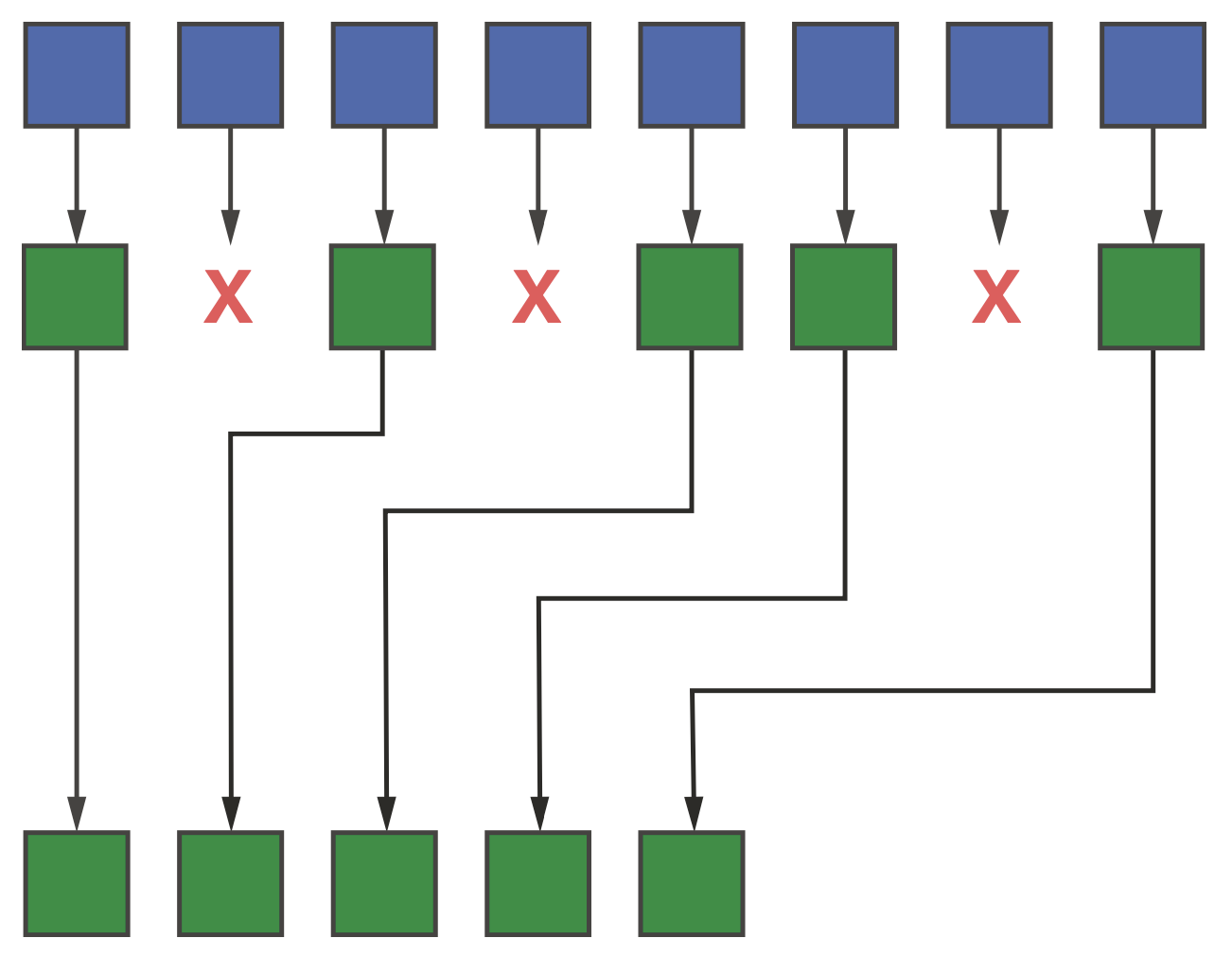
Pack模式根据一个条件丢弃一些元素,并将剩下元素pack到输出范围的连续位置,如下图所示。
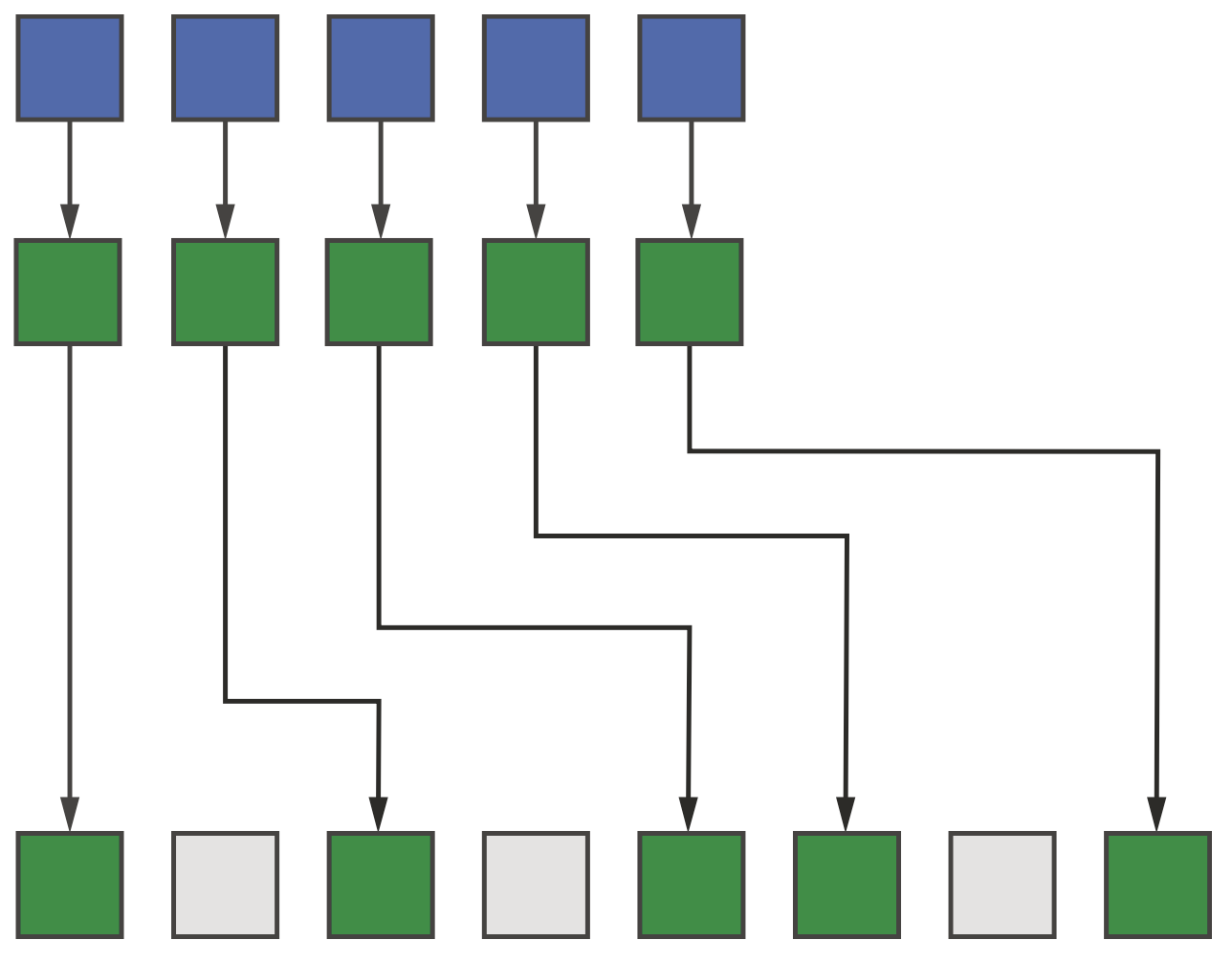
Unpack模式则相反,输入范围的连续元素被unpack到输出范围的非连续位置,如下图所示。
使用DPC++函数和库
DPC++ Reduction库
下面是一个说明如何使用reduction库的数据并行kernel的例子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <CL/sycl.hpp>
#include <iostream>
#include <numeric>
using namespace sycl;
int main() {
constexpr size_t N = 16;
constexpr size_t B = 4;
queue Q;
int* data = malloc_shared<int>(N, Q);
int* sum = malloc_shared<int>(1, Q);
std::iota(data, data + N, 1);
*sum = 0;
Q.submit([&](handler& h) {
h.parallel_for(
nd_range<1>{N, B},
reduction(sum, plus<>()),
[=](nd_item<1> it, auto& sum) {
int i = it.get_global_id(0);
sum += data[i];
});
}).wait();
std::cout << "sum = " << *sum << "\n";
bool passed = (*sum == ((N * (N + 1)) / 2));
std::cout << ((passed) ? "SUCCESS" : "FAILURE") << "\n";
free(sum, Q);
free(data, Q);
return (passed) ? 0 : 1;
}
下面是reduction类的函数原型,我们可以通过下面的函数来构造一个reduction对象。
1
2
3
4
5
template <typename T, typename BinaryOperation>
unspecified reduction(T* variable, BinaryOperation combiner);
template <typename T, typename BinaryOperation>
unspecified reduction(T* variable, T identity, BinaryOperation combiner);
下面是reducer类的简化定义,对reduction暴露了有限的接口,避免我们通过任何可能不安全的方式来更新reduction变量。
1
2
3
4
5
6
7
8
9
10
11
template <typename T,
typename BinaryOperation,
/* implementation-defined */>
class reducer {
// Combine partial result with reducer's value
void combine(const T& partial);
};
// Other operators are available for standard binary operations
template <typename T>
auto& operator +=(reducer<T,plus::<T>>&, const T&);
用户也可以定义简单的reduction,如下面的例子展示了如何使用用户定义reduction来计算一个向量中的最小元素及其位置。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <CL/sycl.hpp>
#include <iostream>
#include <random>
using namespace sycl;
template <typename T, typename I>
struct pair {
bool operator<(const pair& o) const {
return val <= o.val || (val == o.val && idx <= o.idx);
}
T val;
I idx;
};
template <typename T, typename I>
using minloc = minimum<pair<T, I>>;
int main() {
constexpr size_t N = 16;
constexpr size_t L = 4;
queue Q;
float* data = malloc_shared<float>(N, Q);
pair<float, int>* res = malloc_shared<pair<float, int>>(1, Q);
std::generate(data, data + N, std::mt19937{});
pair<float, int> identity = {
std::numeric_limits<float>::max(), std::numeric_limits<int>::min()};
*res = identity;
auto red = sycl::reduction(res, identity, minloc<float, int>());
Q.submit([&](handler& h) {
h.parallel_for(nd_range<1>{N, L}, red, [=](nd_item<1> item, auto& res) {
int i = item.get_global_id(0);
pair<float, int> partial = {data[i], i};
res.combine(partial);
});
}).wait();
std::cout << "minimum value = " << res->val << " at " << res->idx << "\n";
pair<float, int> gold = identity;
for (int i = 0; i < N; ++i) {
if (data[i] <= gold.val || (data[i] == gold.val && i < gold.idx)) {
gold.val = data[i];
gold.idx = i;
}
}
bool passed = (res->val == gold.val) && (res->idx == gold.idx);
std::cout << ((passed) ? "SUCCESS" : "FAILURE") << "\n";
free(res, Q);
free(data, Q);
return (passed) ? 0 : 1;
}
oneAPI DPC++库
C++ STL有几种算法与之前讨论的并行模式相对应,且从C++17开始,可以支持一个执行策略参数,表示这些算法应该串行还是并行执行。oneAPI DPC++库(oneDPL)借此提供了一种高效的并行编程方法,如果一个程序可以完全使用STL算法的功能来表达,那么oneDPL就有可能利用系统中的加速器,而无需编写DPC++ kernel代码。
并行模式的简单实现
Map
1
2
3
Q.parallel_for(N, [=](id<1> i) {
output[i] = sqrt(input[i]);
}).wait();
Stencil
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
buffer<float, 2> input_buf(input.data(), alloc_range);
buffer<float, 2> output_buf(output.data(), alloc_range);
Q.submit([&](handler& h) {
accessor input{ input_buf, h };
accessor output{ output_buf, h };
// Compute the average of each cell and its immediate neighbors
h.parallel_for(stencil_range, [=](id<2> idx) {
int i = idx[0] + 1;
int j = idx[1] + 1;
float self = input[i][j];
float north = input[i - 1][j];
float east = input[i][j + 1];
float south = input[i + 1][j];
float west = input[i][j - 1];
output[i][j] = (self + north + east + south + west) / 5.0f;
});
});
需要注意的是,上面的代码只是最简单的实现,但我们可以利用work-group本地内存来减少内存访问,提高性能,如下所示。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
// Create SYCL buffers associated with input/output
buffer<float, 2> input_buf(input.data(), alloc_range);
buffer<float, 2> output_buf(output.data(), alloc_range);
Q.submit([&](handler& h) {
accessor input{ input_buf, h };
accessor output{ output_buf, h };
constexpr size_t B = 4;
range<2> local_range(B, B);
range<2> tile_size = local_range + range<2>(2, 2); // Includes boundary cells
auto tile = local_accessor<float, 2>(tile_size, h);
// Compute the average of each cell and its immediate neighbors
h.parallel_for(
nd_range<2>(stencil_range, local_range), [=](nd_item<2> it) {
// Load this tile into work-group local memory
id<2> lid = it.get_local_id();
range<2> lrange = it.get_local_range();
for (int ti = lid[0]; ti < B + 2; ti += lrange[0]) {
int gi = ti + B * it.get_group(0);
for (int tj = lid[1]; tj < B + 2; tj += lrange[1]) {
int gj = tj + B * it.get_group(1);
tile[ti][tj] = input[gi][gj];
}
}
it.barrier(access::fence_space::local_space);
// Compute the stencil using values from local memory
int gi = it.get_global_id(0) + 1;
int gj = it.get_global_id(1) + 1;
int ti = it.get_local_id(0) + 1;
int tj = it.get_local_id(1) + 1;
float self = tile[ti][tj];
float north = tile[ti - 1][tj];
float east = tile[ti][tj + 1];
float south = tile[ti + 1][tj];
float west = tile[ti][tj - 1];
output[gi][gj] = (self + north + east + south + west) / 5.0f;
});
});
Reduction
Reduction的实现稍显复杂,需要利用work-item之间同步和通信的语言特性(如原子操作、work-groupo和sub-group函数、shuffle函数等),下面的代码是两种可能的实现方式,第一种是最简单的实现,对每个work-item使用基本的parallel_for和原子操作,第二种进行了简单的优化,分别使用ND-range parallel_for和work-group reduce函数。
1
2
3
4
5
6
7
Q.parallel_for(N, [=](id<1> i) {
ext::oneapi::atomic_ref<
int,
memory_order::relaxed,
memory_scope::system,
access::address_space::global_space>(*sum) += data[i];
}).wait();
1
2
3
4
5
6
7
8
9
10
11
Q.parallel_for(nd_range<1>{N, B}, [=](nd_item<1> it) {
int i = it.get_global_id(0);
int group_sum = reduce_over_group(it.get_group(), data[i], plus<>());
if (it.get_local_id(0) == 0) {
ext::oneapi::atomic_ref<
int,
memory_order::relaxed,
memory_scope::system,
access::address_space::global_space>(*sum) += group_sum;
}
}).wait();
Scan
实现并行scan需要对数据多次scan,每次scan之间都要进行同步。由于DPC++没有提供同步ND-range中所有work-item的机制,直接实现设备范围内的scan必须使用多个kernel来实现,并使用全局内存共享中间结果。下面的代码展示了使用三个kernel来实现scan,这三个kernel对应了之前介绍scan模式的图中的三个层次。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
// Create a temporary allocation that will only be used by the device
int32_t* tmp = malloc_device<int32_t>(G, q);
// Phase 1: Compute local scans over input blocks
q.submit([&](handler& h) {
auto local = local_accessor<int32_t, 1>(L, h);
h.parallel_for(nd_range<1>(N, L), [=](nd_item<1> it) {
int i = it.get_global_id(0);
int li = it.get_local_id(0);
// Copy input to local memory
local[li] = input[i];
it.barrier();
// Perform inclusive scan in local memory
for (int32_t d = 0; d <= log2((float)L) - 1; ++d) {
uint32_t stride = (1 << d);
int32_t update = (li >= stride) ? local[li - stride] : 0;
it.barrier();
local[li] += update;
it.barrier();
}
// Write the result for each item to the output buffer
// Write the last result from this block to the temporary buffer
output[i] = local[li];
if (li == it.get_local_range()[0] - 1) {
tmp[it.get_group(0)] = local[li];
}
});
}).wait();
// Phase 2: Compute scan over partial results
q.submit([&](handler& h) {
auto local = local_accessor<int32_t, 1>(G, h);
h.parallel_for(nd_range<1>(G, G), [=](nd_item<1> it) {
int i = it.get_global_id(0);
int li = it.get_local_id(0);
// Copy input to local memory
local[li] = tmp[i];
it.barrier();
// Perform inclusive scan in local memory
for (int32_t d = 0; d <= log2((float)G) - 1; ++d) {
uint32_t stride = (1 << d);
int32_t update = (li >= stride) ? local[li - stride] : 0;
it.barrier();
local[li] += update;
it.barrier();
}
// Overwrite result from each work-item in the temporary buffer
tmp[i] = local[li];
});
}).wait();
// Phase 3: Update local scans using partial results
q.parallel_for(nd_range<1>(N, L), [=](nd_item<1> it) {
int g = it.get_group(0);
if (g > 0) {
int i = it.get_global_id(0);
output[i] += tmp[g - 1];
}
}).wait();
Pack和Unpack
由于pack依赖于scan,适用于ND-range中所有元素的pack也必须通过全局内存和多个kernel来实现。然而,有一个常见的情况是只对特定的work-group或sub-group内的pack,不需要对ND-range内所有元素进行操作。原书中给出了一个实际的例子,可以参考源代码。Unpack和pack同理,同样依赖于scan,也可以参考原书中给出的例子。